Inscription / Connexion Nouveau Sujet
2 cellule RC en parallèle
Bonjour,
J'ai un exercice qui me pose problème.
Soit un circuit réalisé par l'association de 2 cellules RC. A t<0, les 2 condo. sont initialemnt chargés à la tension U0.
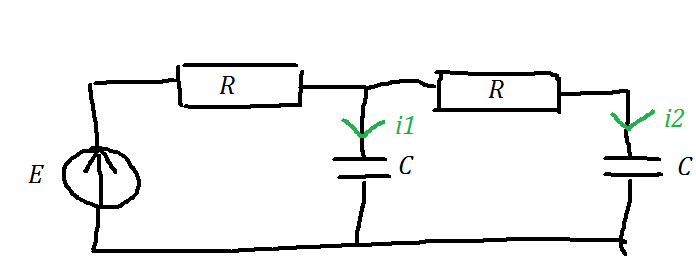
Schéma : 1er branche : un générateur E + résistance R
2eme branche : un condo C + un courant i1
3eme branche : une résistance R + un condo C + un courant i2
Rien que la première question me pose problème.
1) Déterminer les conditions initiales i1(0), i2(0) et di2(0)/dt
Je ne sais pas quel loi appliquer, car dans la suite de l'exercice on me demande une équa diff avec du i2.
Donc je suppose qu'il faut un loi des noeuds, mais il manque quand même quelque chose.
Merci d'avance !
Lorsque l'on te demande des conditions initiales, il faut utiliser la continuité de la tension (resp. courant) aux bornes de la capa (resp inductance).
Oui je suis d'accord mais pour la dérivée, il faut établir une équation, non ?
Et juste le 'resp' j'ai pas compris.
En effet.
Il y a une petite règle très pratique qui dit que le nombre de CI est donné parle nombre de capas, inductances.
Le resp signifie respectivement : continuité du courant circulant dans une inductance.
Oui, entièrement d'accord.
J'ai appliqué une loi des noeuds et des mailles, et je trouve i1(0)=(E+U0)/R et i2(0)=-U0/R
C'est possible ?
J'ai du mal comprendre ton circuit. La tension me semble nulle aux bornes de la résistance de la 3eme branche à t=0.
Oui la description ne dois pas être très au point.
Non je ne pense pas que la tension soit nul.
Mais est-ce que mes conditions initiales sont justes ?
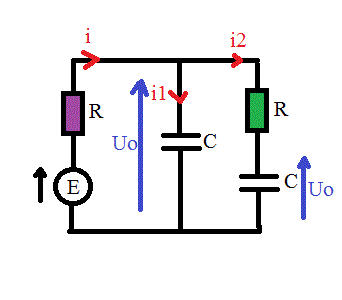
C'est la situation en t = 0.
Equation de la maille avec les 2 condensateurs et la résistance verte :
Uo - R.i2 - Uo = 0
R.i2 = 0
Et donc i2(0) = 0
Equation de la maille avec E , Rmauve et C de la branche centrale :
E - R.i - Uo = 0
i = (E - Uo)/R
Equation du noeud (sur le haut du schèma):
i = i1 + i2
Et donc :
(E - Uo)/R = i1 + 0
i1(0) = (E - Uo)/R
-----
Sauf distraction. 
Merci, de m'avoir consacré de votre temps.
Mais j'aimerai avoir encore un petit coup de pouce.
Comment je fais pour avoir une équation différentielle avec i2(t).
Sachant qu'en cours nous avons traité exclusivement des sujets où l'équation était donné par la tension du condensateur.
E - Ri = Uc1 (avec Uc1 la tension sur le C de la branche centrale)
Uc1 = R.i2 - Uc2 (avec Uc2 la tension sur le C de la branche de droite)
i1 = C.dUc1/dt
i2 = C.dUc2/dt
i = i1 + i2
---
On élimine i :
E - Ri1 - R.i2 = Uc1
Uc1 = R.i2 - Uc2
i1 = C.dUc1/dt
i2 = C.dUc2/dt
---
On élimine Uc1
E - Ri1 - R.i2 = R.i2 - Uc2
i1 = RC.di2/dt - dUc2/dt
i2 = C.dUc2/dt
---
On élimine i1 :
E - R(RC.di2/dt - dUc2/dt) - R.i2 = R.i2 - Uc2
i2 = C.dUc2/dt
---
E - R(RC.di2/dt - dUc2/dt) - 2R.i2 = - Uc2
i2 = C.dUc2/dt
---
En dérivant E - R(RC.di2/dt - dUc2/dt) - 2R.i2 = - Uc2 :
-R²C d²i2/dt² + R.d²Uc2/dt² - 2R.di2/dt = - dUC2/dt
i2 = C.dUc2/dt
---
On élimine Uc2
-R²C d²i2/dt² + R.di2/dt - 2R.di2/dt = - i2/C
---
R²C² d²i2/dt² + RC.di2/dt + i2 = 0
-----
Sans aucune relecture ... Donc à vérifier.
Recopier sans comprendre est inutile.

Je ne remets pas en cause votre raisonnement, il est juste.
Mais je ne comprend pas comment vous passez de -R²C d²i2/dt² + R.d²Uc2/dt² - 2R.di2/dt = - dUC2/dt à -R²C d²i2/dt² + R.di2/dt - 2R.di2/dt = - i2/C
Parce que moi, j'ai refais le calcul dans mon coin et je ne trouve pas votre résultat.
Je trouve : -R²C d²i2/dt² + R/C.di2/dt - 2R.di2/dt = - i2/C avec di2/dt = C.d²Uc2/dt
C'est parce qu'il manque un "C" dans une ligne du début.
J'aui écrit : i1 = RC.di2/dt - dUc2/dt
au lieu d'écrire : i1 = RC.di2/dt - C.dUc2/dt
Plus loin, on arrive alors à :
-R²C d²i2/dt² + RC.d²Uc2/dt² - 2R.di2/dt = - dUC2/dt
i2 = C.dUc2/dt
di2/dt = C.d²Uc2/dt² --->
-R²C d²i2/dt² + R.di2/dt - 2R.di2/dt = - i2/C

J'ai encore décelé une petite erreur. Mais sinon, à la fin j'ai trouvé le bon résultat.
-> E - R.i = Uc1 (petite maille de gauche)
-> E - RC.dUc1/dt - R.i2 = R.i2 + Uc2 (Uc1 = Ri2+Uc2 et i=i1+i2 et i1=C.dUc1/dt)
-> E - R²C².di2/dt - RC.dUc2/dt - R.i2 = R.i2 + Uc2 (i1 = C.dUc1/dt = C.d/dt(Ri2 + Uc2) = RC.di2/dt + C.dUc2/dt)
-> - R²C².d²i2/dt² - RC.d²Uc2/dt² - R.di2/dt = R.di2/dt + dUc2/dt (on multiplie par d/dt)
-> - R²C².d²i2/dt² - R.di2/dt - R.di2/dt = R.di2/dt + i2/C (i2 = C.dUc2/dt di2/dt = C.d²Uc2/dt²)
-> Après on met en forme et sa donne : d²i2/dt + 3/ .di2/dt + 1
.di2/dt + 1 ².i2 = 0 avec
².i2 = 0 avec  = RC
= RC
Et encore merci ! 
Rien n'est jamais parfait, petit erreur ligne 3 dans la parenthèse.
-> (dUc1/dt = d/dt(Ri2 + Uc2) = R.di2/dt + dUc2/dt)
Et idem pour le - R²C².di2/dt. Il n'y a pas de "²" sur le C jusqu'à la dernière étape.
Je corrige une erreur de signe dans mon message originel :
E - Ri = Uc1 (avec Uc1 la tension sur le C de la branche centrale)
Uc1 = R.i2 + Uc2 (avec Uc2 la tension sur le C de la branche de droite)
i1 = C.dUc1/dt
i2 = C.dUc2/dt
i = i1 + i2
-----
On élimine i :
E - Ri1 - R.i2 = Uc1
Uc1 = R.i2 + Uc2
i1 = C.dUc1/dt
i2 = C.dUc2/dt
---
On élimine Uc1
E - Ri1 - R.i2 = R.i2 + Uc2
i1 = RC.di2/dt + C.dUc2/dt
i2 = C.dUc2/dt
---
On élimine i1 :
E - R(RC.di2/dt + C.dUc2/dt) - R.i2 = R.i2 + Uc2
i2 = C.dUc2/dt
---
E - R(RC.di2/dt + C.dUc2/dt) - 2R.i2 = Uc2
i2 = C.dUc2/dt
---
En dérivant E - R(RC.di2/dt + C.dUc2/dt) - 2R.i2 = Uc2 :
-R²C d²i2/dt² - RC.d²Uc2/dt² - 2R.di2/dt = dUC2/dt
i2 = C.dUc2/dt
---
On élimine Uc2
-R²C d²i2/dt² - R.di2/dt - 2R.di2/dt = i2/C
---
R²C² d²i2/dt² + 3.RC.di2/dt + i2 = 0
d²i2/dt² + (3/(RC)).di2/dt + (1/(RC)²).i2 = 0
-----
Cette fois -ci, avec relecture. 


