Salut

Bon j'ai pas cherché à comprendre les expressions de x' et t', mais pour trouver le résultat final, il suffit de faire le rapport des deux dérivées (dx'/dt et dt'/dt).

Si tu regardes bien, l'élément différentiel "dt" se simplifie, et tu obtiens dx'/dt'

Si t'es en terminale, tu trouves peut être ça bizarre de simplifier par dt, étant donné qu'en maths on utilise la notation f'(x) et pas df/dx.
Mais je t'assure qu'on peut le faire

Et si tu comprends pas et que ça t'intéresse je peux essayer de t'expliquer^^

D'accord, merci j'ai compris !
Par contre oui ca m'intéresse je veux bien un petit peu plus d'explications, on ne manipule effectivement que très peu les dérivées sous la forme dx/dt en terminale.

Okai

Alors une fonction f(x) exprime physiquement une relation entre deux grandeurs : x et f.

Comme ces grandeurs sont liées, si l'une varie, l'autre varie aussi (sauf si f(x) = cte bien sûr ! )
Pour traduire cette variation relative (variation de l'une par rapport à l'autre) on utilise la notion de dérivée.

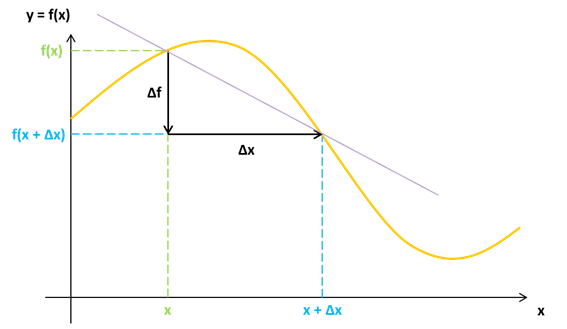
Admettons pour commencer que x varie de x à x + x : dans ce cas, f varie de f(x) à f(x + x) (voir image 1).

Les variations sont :
- x (elle peut être négative !)
- f = f(x + x) - f(x) (elle peut aussi être négative !)

Pour traduire la variation de f par rapport à celle de x, il suffit de donner le rapport , qui est le coefficient directeur de la droite passant par les deux points (celle en violet sur le schéma).

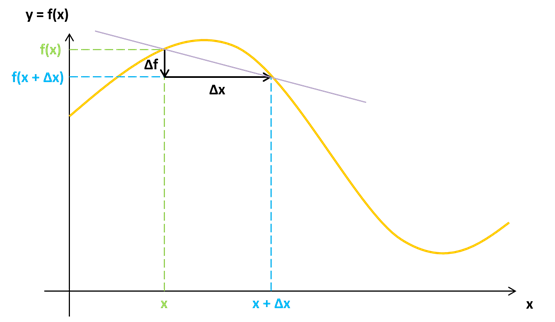
Mais si tu réfléchies bien, pour chaque valeur de x (donc en fonction de la distance par rapport à x), tu auras un coefficient directeur différent (donc une variation de f par rapport à x différente) (voir image 2).

Parmi toutes ces valeurs possibles (une infinité), la seule qui nous intéresse, et qu'on appellera "nombre dérivé en x", c'est celle qui se trouve au voisinage de x.
Autrement dit, on s'intéresse à la variation de f par rapport à x, quand x varie très très peu.

D'une certaine façon, on peut dire que c'est la limite de quand x tend vers 0.
Donc : .

Ça c'est ce que t'as vu en maths normalement

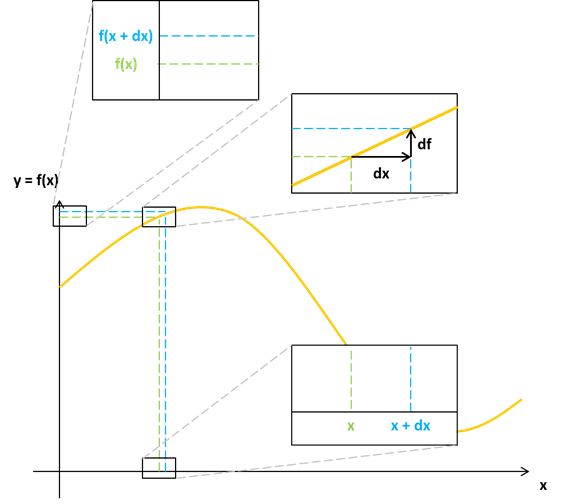
Maintenant tu peux aussi imaginer une variation infinitésimale de x, qu'on notera dx (qui peut être négative !).
Dans ce cas, f subit une variation df = f(x + dx) - f(x) (qui peut aussi être négative !).

Comme dx est extrêmement petit, on peut considérer que la fonction est une droite (voir image 3) et correspond à la tangente de la fonction f au point d'abscisse x.
On en déduit que : .

Donc en fait c'est un peu le même raisonnement dans les deux cas^^
Dans le deuxième cas, on a pas besoin de limite, puisque dx est déjà infiniment petit

Pour info : dx et df sont appelés "éléments différentiels", et ils donnent leur nom aux équations différentielles (je sais pas si elles sont revenues au programme de lycée ou pas^^).

Woaw merci pour cette énorme explication !
Je l'ai relu 4 fois pour tout comprendre mais la ça me fait une véritable révélation sur les mystérieux dx et df ! En classe on ne nous explique pas ce que c'est, on doit juste l'utiliser sans savoir ce que c'est.

Non je ne crois pas que l'on fasse les équations différentielles cette année.

En tout cas merci infiniment pour cette explication qui a du vous prendre beaucoup de temps à écrire, et les schémas rendent ca bien plus claire.

La seule chose que j'ai pas tout a fait comprise, c'est la transition entre
et

J'ai compris le principe théorique avec le coefficient directeur de la tangente etc... Mais je ne comprend pas comment vous êtes passé d'une expression à l'autre sous forme mathématique.

Derien

Ouai, c'était pas non plus au programme quand j'y étais... c'est bien dommage parce que quand on est amenés à en faire après, on est un peu perdus au début x)

Il n'y a pas vraiment de transition entre les deux formules que tu as écrites

Par définition, df est la variation de f, quand x varie de x à x + dx.
Autrement dit : df = f(x + dx) - f(x).

La variation de x est dx, et celle de f est df : la variation de f par rapport à celle de x est donc (même raisonnement que pour f et x).

Sauf qu'on a pas besoin de faire la limite quand dx tend vers 0 (comme on l'avait fait pour x), puisque dx est déjà infiniment petit !

Donc on peut directement écrire le nombre dérivé ^^

En conclusion :
- pour une grande variation x, on est obligés de la faire tendre vers 0
- pour une variation infinitésimale dx, c'est pas la peine

Donc :

C'est mieux ?

dx'/dt' = (dx'/dt ) * (dt'/dt)

Donc en ayant déterminé dx'/dt et dt'/dt ... on a facilement dx'/dt'
-----
Soit ...

Néanmoins, je serais intéressé de s'avoir comment, à partir de l'expression x' = ... de ton énoncé ne contenant pas de "v", tu arrives à trouver l'expression de dx'/dt = ... qui elle contient des "v".

Même remarque pour trouver dt'/dt qui, pour toi, dépend de "v" alors que l'éxpression de t' = f(t) ne contient pas de v.

Bref, il me semble qu'il y a de la bisbrouille dans ton message.

Sauf distraction.  

Zut, lire :

dx'/dt' = (dx'/dt ) /(dt'/dt) dans mon message précédent.

Derien

Bonne continuation

dx'/dt' = (dx'/dt ) /(dt'/dt)

dx'/dt' = (c-u)/(1 - u/c)

dx'/dt' =  (c-u)/[(c - u)/c]

dx'/dt' = c

Sauf distraction.