Inscription / Connexion Nouveau Sujet
position d"équilibre
Bonjour
Pour une vérification et une aide
la tige (de longueur l avec une masse m au bout) d'un métronome est écartée d'un angle 
Epp = -mgl(1-cos ) bon ? le moins est bon ?
) bon ? le moins est bon ?
Epe= 1/2k ² donnée
² donnée
Pour avoir les positions d'équilibre on dérive l'énergie potentielle et on l'annule :
d(Epe+Epp)/dt=0
soit l(d /dt)
/dt) +mgl(d
+mgl(d /dt)sin
/dt)sin =0
=0
on divise par d /dt qui est différent de 0
/dt qui est différent de 0
soit k -mglsin
-mglsin =0
=0
aprés comme résoudre ?
Merci si vous pouvez m'aider
Bonjour
le moins est bon ?
N'ayant pas la figure, difficile de donner une réponse "certaine" mais a priori tu as raison si tu as choisi l'origine des énergies potentielle nulle à la position
 =O.
=O.
Pour comprendre la situation commence par superposer graphiquement la droite d'équation Y1=k.
 et la sinusoïde d'équation Y2=mgl.sin(
et la sinusoïde d'équation Y2=mgl.sin( ) pour
) pour  compris entre -
compris entre - et
et  dans les deux cas : k
dans les deux cas : k mgl puis k<mgl
mgl puis k<mgl
Tu verras que l'on obtient soit une solution (évidente !) soit trois solutions dont une évidente.
Trace ensuite l'allure de la courbe Ep =f(
 ) dans chacun des deux cas évoqués. Dans un cas, tu as une seule position d'équilibre et elle est stable ; dans l'autre cas, tu as une position d'équilibre instable et deux positions d'équilibre stables symétriques par rapport à la verticale.
) dans chacun des deux cas évoqués. Dans un cas, tu as une seule position d'équilibre et elle est stable ; dans l'autre cas, tu as une position d'équilibre instable et deux positions d'équilibre stables symétriques par rapport à la verticale.
Une des solutions est évidente. Pour les deux autres, il n'y a pas de solution explicite exacte. Tu peux te contenter d'une simulation numérique ou, si la valeur de mgl n'est que de très peu supérieure à k, tu peux effectuer un développement limité de sin(
 ) au voisinage de
) au voisinage de  = 0.
= 0.Merci
Effectivement pour l'origine : la tige est écartée vers le bas de  et remonte vers le haut pour rejoindre
et remonte vers le haut pour rejoindre  =0
=0
Il n-y a pas une solution mathématiques sans graphique ?
Désolé pour toi : il n'existe pas de solution mathématique explicite à l'équation : sin(x) = C.x (C : réel positif) sauf bien sûr la solution évidente que j'ai évoquée précédemment !
La méthode graphique a l'avantage de faire réfléchir aux différentes situations physiques envisageables suivant la raideur plus ou moins importante du ressort spiral... J'imagine que tu t'attendais à une réponse  = AAA (formule) ; désolé : la réalité physique est plus compliquée...
= AAA (formule) ; désolé : la réalité physique est plus compliquée...
Au fait : quelle est la question exacte posée ? Si tu as des valeurs numériques fournies, la solution à retenir est peut-être la solution évidente que j'ai évoquée précédemment...
Les questions étaient :
1 déterminer l'expression de Epp
2 Déterminer la dimension de la raideur k et
3 ou j'en suis :
En déduire l'expression de la ou des positions d'équilibre, mais on peut pas déduire cela de la 2.....?
Ensuite à la 4 il faut déterminer la position d'équilibre pour k/mgl >=1 qui est unique.
Ensuite j'étudierai sa stabilité...
Et enfin un une résolution par dichotomie pour les 3 autres. mais j'en suis pas encore la mais je vais y réfléchir.....
Merci pour votre aide
Merci beaucoup je continue seul et ensuite si je suis bloqué ou besoin de confirmation je poste...
Encore merci pour ton aide
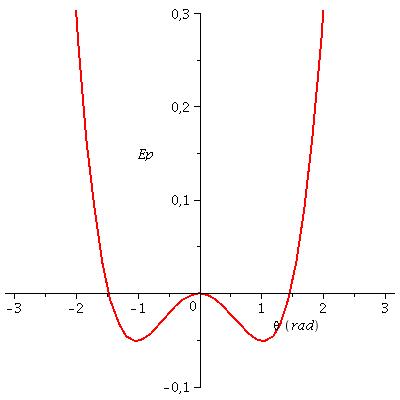
Cela t'aidera peut-être : voici les courbes Ep = f( ) dans deux cas particuliers (échelle arbitraire pour Ep) :
) dans deux cas particuliers (échelle arbitraire pour Ep) :
1° cas : mgl=1,2.k : on obtient une position d'équilibre instable en  =0 et deux positions d'équilibre stables symétriques par rapport à la verticale ;
=0 et deux positions d'équilibre stables symétriques par rapport à la verticale ;
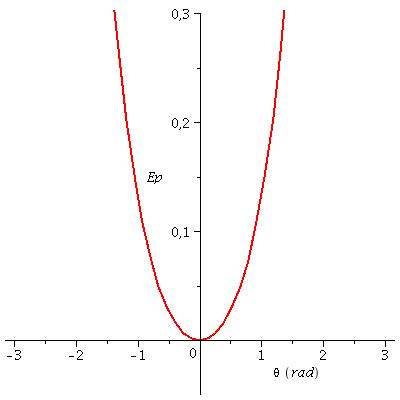
2° cas : mgl = 0,8.k : on obtient une seule position d'équilibre en  =0 et elle est stable.
=0 et elle est stable.
Je te laisse justifier tout cela...
Je vois pas comment tu as tracé les courbe de Ep=f ( ) à partir de : mgl=1,2.k par exemple pour la première. Ou est
) à partir de : mgl=1,2.k par exemple pour la première. Ou est  et sin (
et sin ( )?
)?
Bonjour,
j'ai posé , dans le cas particulier mgl = 1,2.k :
Pour avoir l'allure de la courbe sans connaître la valeur numérique de k, j'ai simplement demandé à mon logiciel de tracer la courbe d'équation :
Évidemment, dans ces conditions, l'ordonnée est proportionnelle à l'énergie potentielle mais n'est pas égale à l'énergie potentielle, d'où la remarque faite à mon message précédent : "échelle arbitraire pour Ep".
Merci j'ai compris le phénomène mais la question 3 de mon exercice me gène dans ce cas :
1 déterminer l'expression de Epp
2 Déterminer la dimension de la raideur k et
3 En déduire l'expression de la ou des positions d'équilibre  èq
èq
Bonsoir,
Si on pose : Ep = f( ), tu as sûrement vu en cours que les positions d'équilibre correspondent à des extremums de f : maximum pour équilibre instable, minimum pour équilibre stable. Tu as déjà qualitativement les réponses à partir des courbes que je t'ai fournies. Mathématiquement, f'(
), tu as sûrement vu en cours que les positions d'équilibre correspondent à des extremums de f : maximum pour équilibre instable, minimum pour équilibre stable. Tu as déjà qualitativement les réponses à partir des courbes que je t'ai fournies. Mathématiquement, f'( )=0 est équivalent à :
)=0 est équivalent à :
k. =mgl.sin(
=mgl.sin( )
)
La solution  =0 est évidente.
=0 est évidente.
Cette solution est la seule possible si k mgl
mgl
si k<mgl les deux autres solutions doivent être obtenues numériquement (programme de dichotomie par exemple) car l'équation n'admet pas de solution explicite mais cela, je te l'ai déjà expliqué !
Oui bien sur c'est ce que j'avais déjà répondu mais je me posais des questions sur cette question posé dans l'exercice et j'avais bien compris hier.
merci beaucoup
Pour étudier la stabilité de la position d"équilibre on dérive deux fois Ep
mais jn'y arrive pas pour  =0 pour k>mgl
=0 pour k>mgl
DEP/DT= k (d
(d /dt)-mgl(d
/dt)-mgl(d /dt)sin
/dt)sin
Je crois que l'on a comme dérivée seconde de Ep en  0=0 :
0=0 :
k-mglsin0 = k-mg>0 donc équilibre stable
Bon ?
encore merci pour votre aide
Bonjour,
Le temps n'intervient pas ici !
Je t'ai expliqué cela dans mes messages précédents !
Il faut étudier la fonction f telle que Ep = f( ) et, comme tu as sans doute l'habitude de le faire, remplir un tableau de variations pour détecter les éventuels maximums et minimums. Tu constateras alors qu'il faut distinguer deux cas :
) et, comme tu as sans doute l'habitude de le faire, remplir un tableau de variations pour détecter les éventuels maximums et minimums. Tu constateras alors qu'il faut distinguer deux cas :
k mgl
mgl
k>mgl
Je vais essayer d"être un peu plus explicite même si l'essentiel a déjà été écrit dans mon premier message du 30-01-16 à 18:35. Il faut aussi que tu revois bien ton cours sur les liens entre les positions d'équilibre et l'énergie potentielle.
mgl étant une constante positive, le signe de la dérivée f'( ) est le signe de :
) est le signe de :
Pour  compris entre -
compris entre - rad et
rad et  rad, on trace la sinusoïde d'équation : Y1=sin(
rad, on trace la sinusoïde d'équation : Y1=sin( )
)
la dérivée de sin( ) par rapport à
) par rapport à  vaut +1 en
vaut +1 en  =0. La tangente en
=0. La tangente en  =0 à la sinusoïde est donc la droite d'équation Y =
=0 à la sinusoïde est donc la droite d'équation Y =  (pointillés noirs).
(pointillés noirs).
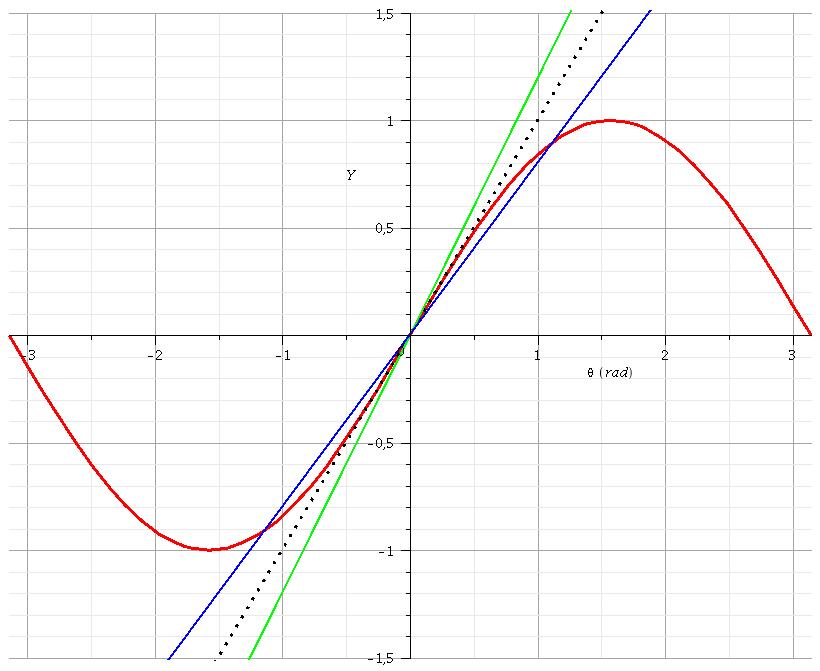
Dans le même repère, on trace la droite d'équation Y2=A. .
.
On remarque : D( )=Y2-Y1.
)=Y2-Y1.
On doit envisager alors deux situations différentes :
A 1 (soit k
1 (soit k mgl : droite en vert) : la droite d'équation Y2=A.
mgl : droite en vert) : la droite d'équation Y2=A. coupe la sinusoïde uniquement en
coupe la sinusoïde uniquement en  =O. La dérivée ne s'annule qu'une seule fois : le système n'a qu'une seule position d'équilibre en
=O. La dérivée ne s'annule qu'une seule fois : le système n'a qu'une seule position d'équilibre en  =0. Il est facile aussi, en regardant pour quelles valeurs de
=0. Il est facile aussi, en regardant pour quelles valeurs de  la droite est au-dessus ou au-dessous de la sinusoïde d'obtenir le signe de la dérivée et donc de remplir un tableau de variation de Ep.
la droite est au-dessus ou au-dessous de la sinusoïde d'obtenir le signe de la dérivée et donc de remplir un tableau de variation de Ep.
A<1 (soit k<mgl : droite en bleu) : la droite coupe la sinusoïde trois fois ; le système a trois positions d'équilibre. Il faut alors remplir un tableau de variation de Ep
Les deux positions d'équilibre stable correspondent à deux valeurs de  opposées. Dans le cas des courbes tracées : la droite en bleu correspond à A = 0,8. On peut constater graphiquement que les abscisses des intersections de cette droite avec la sinusoïde sont de l'ordre de
opposées. Dans le cas des courbes tracées : la droite en bleu correspond à A = 0,8. On peut constater graphiquement que les abscisses des intersections de cette droite avec la sinusoïde sont de l'ordre de  1,1rad. Pour être plus précis, il faut utiliser un programme de résolution numérique d'équation (dichotomie par exemple) qui conduit à
1,1rad. Pour être plus précis, il faut utiliser un programme de résolution numérique d'équation (dichotomie par exemple) qui conduit à  1,1311rad (à toi d'arrondir en fonction de la précision des données).
1,1311rad (à toi d'arrondir en fonction de la précision des données).
Remarque : Je ne sais pas si tu as étudié en math les développements limités de Taylor. Si oui, il est possible d'obtenir une "formule" (ce que tu cherches depuis le début !) permettant d'obtenir les positions d'équilibre stable mais cela, seulement si A est peu inférieur à 1. L'expression approchée de sin( ) est :
) est :
Les positions d'équilibre stable correspondent alors à :
L'approximation est d'autant meilleure que la valeur de A est proche de 1 par valeurs inférieures.
Merci beaucoup pour cet exposé, je viens de me replonger dedans.
Pour la stabilité des équilibre, les courbe de Epp suffisent (j'ai bien compris comment on les obtenais) ou faut il mieux étudier la dérivée seconde ?
Bonjour,
Les courbes Ep=f ) suffisent à condition que leurs allures soient correctement justifiées à l'aide de tableau de variations avec étude des signes de dEp/d
) suffisent à condition que leurs allures soient correctement justifiées à l'aide de tableau de variations avec étude des signes de dEp/d .
.
L'étude à partir du signe des dérivées secondes est très intéressante lorsqu'on ne veut pas tracer les courbes Ep=f ) . A mon avis tu as là deux méthodes différentes ayant le même but : il faut utiliser l'une ou l'autre.
) . A mon avis tu as là deux méthodes différentes ayant le même but : il faut utiliser l'une ou l'autre.
Enfin : ceci est mon avis : fais comme le demande ton professeur !
C'est la dérivée par rapport à théta ou par rapport au temps.
De manière générale quand fait-on la dérivée par rapport au temps ou par rapport à théta ?
Merci
Si je me trompe pas la dérivé par rapport au temps c'est pour des variations temporelles tel que la conservation de l'énergie mécanique.
L'étude de l'équilibre se fait en étudiant les maximums ou minimum de Ep par rapport à  . Le temps n'intervient pas lors de la recherche des positions d'équilibre.
. Le temps n'intervient pas lors de la recherche des positions d'équilibre.
Dans mes messages précédents, j'ai toujours écrit : Ep = f( ) et l'axe horizontal des repères de mes courbes porte toujours l'indication :
) et l'axe horizontal des repères de mes courbes porte toujours l'indication :  (rad), pas l'indication : "t" !
(rad), pas l'indication : "t" !
Après application du théorème de l'énergie mécanique on a :
d2 (thêta)/dt2+(k/ml)thêta +gsin(thêta)=0
Soit pour petit angle :
On supprime sinthêta=0
comment résoudre
d2 (thêta)/dt2+(k/ml)thêta =0 par la méthode d'Euler ?
Merci beaucoup
Bonsoir
après application de la conserva de lEm
d2 (thêta) /dt2 + (k/ml) theta+[strike][/strike]gsin (thêta)=0
Pour angle petit
On supprime gsin (thêta)
Comment résoudre par la méthode d'Euler
d2 (thêta) /dt2 + (k/ml) theta =0
Merci beaucoup
Bonsoir
Comment résoudre par la méthode d'Euler
d2 (thêta) /dt2 + (k/ml) theta =0
Je crois que cette équation est fausse. Je reprends à partir de la conservation de l'énergie mécanique :
Les constantes
 max et
max et  dépendent des conditions initiales. On obtient un mouvement circulaire sinusoïdal de période propre
dépendent des conditions initiales. On obtient un mouvement circulaire sinusoïdal de période propre Pour k<mgl : on obtient aussi des oscillations autour d'une position d'équilibre stable mais la mise en équation est plus complexe car l'approximation sin(
 )
)
 n'est pas nécessairement possible.
n'est pas nécessairement possible.
La résolution numérique d'une équation différentielle par la méthode d'Euler présente un intérêt quand cette équation n'admet pas de solution explicite. Ce n'est pas le cas ici !
Que signifie la phrase :
"Effectivement pour l'origine : la tige est écartée vers le bas de theta et remonte vers le haut pour rejoindre theta=0" ?
Voila une photo d'un certain type de métronome :

Parfois, la masse en bas est cachée par le boîtier ... mais est quand même présente.
S'il s'agit d'un tel type de métronome (masse du bas cachée ou non), alors il faut connaître les valeurs de la masse du bas, de la masse du haut, de la masse de la tige, l'emplacement du point de pivot sur la tige, la position du centre d'inertie de la masse du bas sur la tige (par rapport au point de pivot) et la position (réglable) du centre d'inertie de la masse du haut sur la tige (par rapport au point de pivot).
Et s'il s'agit d'un pendule simple (rare pour un métronome), il faut quand même connaître la masse de la tige (dont l'effet n'est pas toujours négligeable comme l'est celui d'un fil ), en plus de la masse suspendue et de sa position sur la tige.
Un énoncé complet (et le croquis qui l'accompagne) serait judicieux avant de spéculer sur ce que pourrait être la réponse attendue.

Merci
J'avais approximé sin(theta) à 0......
Je ne vois pas pourquoi l'énoncé me demande d'appliquer la methode d'Euler.....car on peut la résoudre sans et de plus on a pas de valeur numériques dans l'énoncé. ?.
Merci
Bonjour,
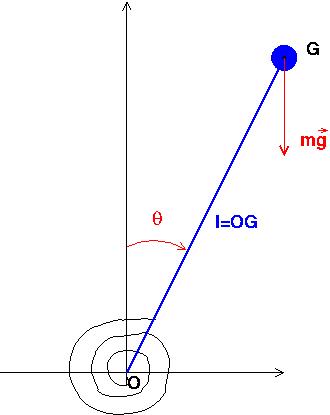
Tout ce qui a été écrit au cours des divers messages est basé sur l'expression de l'énergie potentielle que tu as fournie dans ton premier message. Cette expression correspond au schéma classique ci-dessous ( mon logiciel ne sais pas tracer un ressort spiral correctement) dans lequel le rayon de la boule de masse m et de centre de gravité G est négligeable devant l = OG. La masse de la tige est négligeable devant m.
Je ne vois pas pourquoi l'énoncé me demande d'appliquer la methode d'Euler
Peut-être que l'amplitude est suffisamment importante pour que l'approximation sin(
 )
)
 soit incorrecte : dans ce cas la méthode d'Euler s'imposerait...
soit incorrecte : dans ce cas la méthode d'Euler s'imposerait...
Bref : un énoncé complet rendrait l'aide plus efficace !
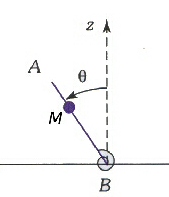
Le m´etronome est constitu´e d'un point mat´eriel de masse m, situ´e en M, pouvant ˆetre d´eplac´e le long d'une tige de masse n´egligeable entre ses deux extr´emit´e A et B. L'extr´emit´e B est fix´ee sur un support. L'ensemble, rigide, est mobile en rotation autour de l'axe ∆ = (Bx), perpendiculaire `a la tige ; on note θ l'angle entre la tige et l'axe verticale (Bz). On admet que l'action subie par la tige en B est une action conservative d'´energie potentielle
Epe= 1/2k 2
2
On se place ici dans le cas ou k/mgl ≥ 1.
1 ´Etudier la stabilit´e de l'unique position d'´equilibre.
2 A l'aide du th´eor`eme de l'´energie m´ecanique, ´etablir l'´equation diff´erentielle v´erifi´ee par θ(t).
La r´esoudre dans le cas o`u les amplitudes sont faibles (il faut, entre autre, pour cela que kmgl soit grand devant 1).
La r´esolution dans le cas g´en´eral pourra se faire num´eriquement `a l'aide de la m´ethode d'euler.
D´eterminer l'expression de la p´eriode d'oscillation en fonction de l. Commenter.
Hormis la liaison en B, le pendule est soumis au poids de la masse ponctuelle en M. On note l la longueur MB que l'utilisateur pourra faire varier. La longueur totale de la tige sera not´ee AB = L
J'avais donc bien "deviné" la totalité de l'énoncé à un détail important près : la situation la moins simple, celle qui correspond à k < mgl n'avait pas à être étudiée (sympa ton professeur !) mais au moins, j'espère que l'étude des deux cas t'aura permis d'approfondir...
Pour la résolution de l'équation différentielle, les choses aussi sont claires : on te demande d'abord d'étudier le cas des amplitudes faibles : c'est la résolution littérale que je t'ai proposée qui conduit à une solution sinusoïdale. On te demande ensuite le cas général d'une amplitude quelconque ; cela signifie qu'il n'est plus possible de remplacer sin( ) par
) par  dans l'équation différentielle et là, une méthode numérique s'impose. Problème : aucune valeur numérique n'est fournie et les conditions initiales ne sont pas précisées.
dans l'équation différentielle et là, une méthode numérique s'impose. Problème : aucune valeur numérique n'est fournie et les conditions initiales ne sont pas précisées.
Reste tout de même un point dont il n'a pas encore été question. Ton énoncé précise d'étudier aussi le cas mgl = k. Pour la résolution numérique avec une amplitude grande, tu peux le traiter en même temps que les cas mgl<k.
En revanche, l'énoncé précise de "résoudre" l'équation différentielle aussi dans le cas particulier mgl = k ; La solution n'est plus sinusoïdale : je ne suis pas sûr que ton professeur ait réalisé la difficulté de cette étude théorique : cela m'étonnerais que les fonctions elliptiques de Jacobi soient à ton programme ! Tu peux sans doute te contenter de dire que le terme (k. -mgl.sin(
-mgl.sin( )) étant très petit sans être tout à fait nul, le retour vers la position d'équilibre stable
)) étant très petit sans être tout à fait nul, le retour vers la position d'équilibre stable  =0 est extrêmement lent...
=0 est extrêmement lent...
Un grand merci. J'ai appris pleins de choses.
Peut être que la méthode d'Euler est juste une ouverture. ...
maintenant je dois écrire un programme python pour résoudre par dichotomie en cherchant 2 flottants a et b pour intervalle de recherche de solution....
sin -
-
 =0
=0
Il aurait été infiniment plus judicieux d'écrire un énoncé complet dès le début au lieu de laisser place à toutes les suppositions.
Non ?

Oui mais on ne dois pas mettre de sujets ici. ..
Qui pourrait m'aider pour écrire une fonction python
pour la fonction
f ( )=sin(
)=sin( )-
)- *
* =0
=0
le but est trouver la solution par dichotomie.
J'ai du mal à différencier
 et
et 
Merci


