Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 3 +

Niveau école ingénieur
Partager :

Mecanique

Posté par
lolo77150 27-07-15 à 17:42

Bonjour l'ile !
Alors j'ai un problème de résolution pour cette exercice :

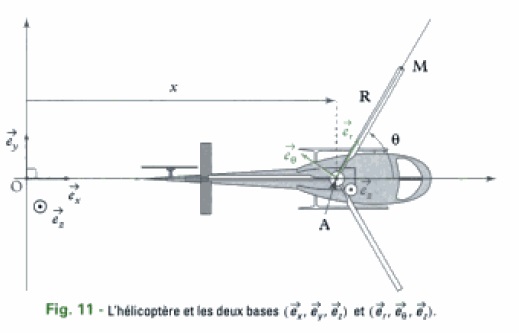
Exprimer le vecteur vitesse du point M dans le référentiel R ( O ; \vec{Ex} ; \vec{Ey} ; \vec{Ez} ) , dans le cas d'un helicoptère comme vu précédemment
Determiner la vitesse limite d'avancement de l'hélicoptère selon l'axe ( O ; \vec{Ev} ) sachant que la vitesse du point M doit être inférieur à la vitesse du son ( Vson = 330 m.s^-1 ) à chaque instant .

Données : Les pales ont un rayon R = 5.3 m et tournent avec une vitesse angulaire :
\omega = \frac{d\teta}{dt} = 450 tr.min^-1

Mecanique

Posté par
lolo77150re : Mecanique 27-07-15 à 17:42

Désolé pour les fractions et vecteur je ne sais pas pourquoi ils ne veulent pas s'afficher

Posté par
Florianbre : Mecanique 27-07-15 à 18:02

Bonjour lolo77150

As-tu déjà vu dans ton cours la loi de composition des vitesses ?

Florian

Posté par
lolo77150re : Mecanique 27-07-15 à 18:10

Bonjour Florian !!

Je viens de lire tout mon cours sur la vitesses et j'ai tout compris , tu parles comment on a la vitesse tout sa ?
En tout cas je viens de lire tout mon cours et sa c'est le 1er exercice d'application

Posté par
Florianbre : Mecanique 27-07-15 à 18:44

Oui, "comment on a la vitesse tout sa"

Tu devrais avoir une loi appelée la loi de composition des vitesses qui fait intervenir les notions de vitesse d'entrainement, vitesse relative et vitesse absolue. Cela te dit quelque chose ? Si c'est le cas, utilise cette relation pour répondre à la question 1).

Florian

Posté par
lolo77150re : Mecanique 27-07-15 à 18:54

Ah non j'ai pas eu sa dans mon cours
J'ai vu que la vitesse c'etais la derivée de la position en plus détaillé c'est tout donc la partie "Vecteur vitesse" et en suite j'ai eu ce petit exo d'application pour les notions que j'avais vu precedement donc vecteur vitesse , vitesse d'un point , vecteur position & trajectoire

Posté par
Florianbre : Mecanique 27-07-15 à 21:30

D'accord.

Dans ce cas là peux-tu écrire les coordonnées du vecteur \vec{OM} dans la base  ( O ; \vec{e_x} ; \vec{e_y} ; \vec{e_z}) ?

Puis applique la formule donnant la vitesse en fonction du vecteur position \vec{OM}.

Florian

Posté par
lolo77150re : Mecanique 27-07-15 à 22:47

\vec{OM} = xEx + yEy

Posté par
lolo77150re : Mecanique 27-07-15 à 22:50

\vec{OM} = x \vec{ex} + y \vec{Ey} *
v=  \frac{d\vec{OM}}{dt} = \vec{ex} + \vec{Ey}

Posté par
Florianbre : Mecanique 28-07-15 à 10:20

Je ne suis pas du tout d'accord avec toi. Décompose le vecteur OM :

OM = OA + AM

Ecrit maintenant les vecteurs OA et AM dans la base (O, ex, ey, ez)

Posté par
lolo77150re : Mecanique 28-07-15 à 10:32

\vec{OA} = x \vec{ex}  
J'ai un doute pour  \vec{AM} , je fais le produit scalaire ?

Posté par
Florianbre : Mecanique 28-07-15 à 10:34

OK pour le vecteur OA. Je ne comprends pas ta question pour le vecteur AM, peux-tu m'expliquer ce que tu entends par faire le produit scalaire ?

Posté par
lolo77150re : Mecanique 28-07-15 à 10:43

Ah non pardon c'est pour trouvé une longueur .
Mais la je sais pas comment je vais procédé pour le \vec{AM}

Posté par
Florianbre : Mecanique 28-07-15 à 10:56

Il faut utiliser la trigonométrie. Regarde le schéma d'un peu plus près (image jointe) et déduis-en les coordonnées du vecteur AM dans le repère (O, ex, ey, ez). Tu connais \theta et R tu peux donc exprimer x_{AM} et y_{AM}. Et attention, comme je te l'avais dis dans un précédent échange, garde bien les valeurs littérales de \theta et R !

Florian

Mecanique

Posté par
lolo77150re : Mecanique 28-07-15 à 11:18

cos( \theta ) = \frac{Xam}{R}  \Longrightarrow Xam = cos(\theta).R
sin( \theta ) = \frac{Yam}{R}  \Longrightarrow Yam = sin(\theta).R

Posté par
Florianbre : Mecanique 28-07-15 à 11:26

Voilà ! Cette "méthode" te sera très souvent utile, penses-y à chaque fois qu'un angle et une projection sur des axes apparaissent.

Écris désormais les coordonnées du vecteur \vec{OM} dans la base  ( O ; \vec{e_x} ; \vec{e_y} ; \vec{e_z}).

Posté par
lolo77150re : Mecanique 28-07-15 à 11:40

Oui effectivement ! j'avais jamais pensé a faire ceci !

\vec{OM} = \vec{OA} + \vec{AM} = x\vec{ex} + cos(\theta).R + sin(\theta).R
Oulala par contre je suis pas du tout sur de comment j'ai ecrit \vec{AM}

Posté par
Florianbre : Mecanique 28-07-15 à 11:45

Oui, \vec{OM} est très mal écrit, c'est même complètement faux (enfin, je comprends ce que tu voulais écrire, et c'est juste, mais la façon dont tu l'as écris est complètement fausse) : on ne mélange pas des vecteurs et des scalaires.

Sur quel axe as-tu projeté AM pour obtenir R.cos(theta) et sur quel axe as-tu projeté AM pour obtenir R.sin(theta) ? (Penses éventuellement à la direction qu'aurait AM si theta valait 0 ou Pi/2 si cela peut t'aider)

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 11:56

Pour obtenir
R.cos(\theta) je l'ai projecter sur l'axe \vec{ex}

Posté par
Florianbre : Mecanique 28-07-15 à 12:04

Pour écrire ça plus correctement (je ne fais pas ça pour t'embêter mais pour que tu es les bonnes méthodes et les bonnes façons de rédiger pour le futur) :

En projetant le vecteur \vec{AM} sur l'axe \vec{e_x} on obtient R.cos(\theta). Autrement dit, R.cos(\theta) est la composante selon x du vecteur \vec{AM}.

Rédige de même pour la composante selon y du vecteur \vec{AM} puis écris le vecteur \vec{AM} dans la base (\vec{e_x} ; \vec{e_y} ; \vec{e_z}).

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 12:13

En projetant le vecteur \vec{AM} sur l'axe \vec{ey} on obtient R.sin(\theta) . R.sin(\theta) est la composante selon y du vecteur \vec{AM}

Posté par
Florianbre : Mecanique 28-07-15 à 13:06

Oui, je suis d'accord avec toi ! Écris maintenant le \vec{AM} puis écris le vecteur \vec{AM} dans la base (\vec{e_x} ; \vec{e_y} ; \vec{e_z}).

Posté par
lolo77150re : Mecanique 28-07-15 à 13:10

\vec{AM} = R.cos(\theta)\vec{ex} + R.sin(\theta)\vec{ey}

Posté par
Florianbre : Mecanique 28-07-15 à 13:18

Parfait !

Pour un tout petit peu plus de rigueur je te conseille même d'écrire :

\vec{AM} = R.cos(\theta(t)) . \vec{e_x} + R.sin(\theta(t)) . \vec{e_y}

Ainsi quand tu dériveras le vecteur \vec{AM} par rapport au temps tu verras tout de suite ce qui dépend du temps et ce qui n'en dépend pas. (tu peux d'ailleurs en faire de même pour le vecteur \vec{OM} en écrivant : \vec{OM} = x(t) . \vec{e_x})

Synthétise désormais tout cela pour exprimer le vecteur \vec{OM} dans la base ( O ; \vec{e_x} ; \vec{e_y} ; \vec{e_z}) puis déduis-en l'expression du vecteur vitesse du point M dans cette même base (tu pourras par exemple le noter \vec{v_{M|R}}.

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 13:39

Oulala j'aurai jamais su que fallait mettre cos(teta) en fonction du temps , j'ai pas trop compris ce truc par conte :p

\vec{OM} = \vec{OA} + \vec{AM} = x(t).\vec{ex} + R.cos(\theta(t)).\vec{ex} + R.sin(\theta(t)).\vec{ey}
v= \frac{d\vec{OM}}{dt}

Posté par
Florianbre : Mecanique 28-07-15 à 13:46

Oui, je suis d'accord avec ton expression de \vec{OM}. Et pour \theta qui est fonction du temps, c'est comme x qui est fonction du temps : les pales de l'hélicoptère tourne donc \theta n'est pas en permanence égal à une valeur donnée.

Et attention dans ce que tu as écris, v est également un vecteur ! On doit donc écrire :

\vec{v} = \dfrac{d\vec{OM}}{dt}

Sachant que tu connais l'expression de \vec{OM} (à nouveau, je te propose d'écrire \vec{OM}(t)) il ne te reste plus qu'à appliquer ta formule. En particulier, souviens toi que :

\dfrac{u(v(x))}{dx} = \dfrac{dv(x)}{dx} * u'(v(x))

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 15:22

Ah daccord !
\vec{v} = (\frac{dx(t).\vec{ex}}{dt}) + (\frac{dR.cos(\theta(t)).\vec{ex}}{dt}) + (\frac{dR.sib(\theta(t)).\vec{ey}}{dt})

\vec{v} = \vec{ex} + (R.(-sin(\theta)).\vec{ex} + (R.cos(\theta)).\vec{ey}
\vec{v} = \vec{ex} + (R.(-cos(\theta)).\vec{ex} + (R.(-sin(\theta)).\vec{ey}

Posté par
Florianbre : Mecanique 28-07-15 à 15:33

Non, ce n'est pas cela.

Allons-y doucement. Si on a x(t), que vaut sa dérivée ? Penses-tu vraiment qu'elle vaut 1 comme tu l'as écrit dans ton dernier message ? Je sais que tu sais faire étant donné l'exercice avec la luge que tu as posté précédemment.

Puis pour cos(\theta(t)) :

Tu es dans le cas où :

u(t) = cos(t) \\ v(t) = \theta(t)

En appliquant la formule que je t'ai rappelée ci-dessus, que vaut alors la dérivée par rapport à t de u(v(t)) ?

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 15:40

x(t) sa derivée est \frac{dx}{dt} non?

Posté par
Florianbre : Mecanique 28-07-15 à 15:46

Oui exactement.

Le début de l'expression de la vitesse est donc :

\vec{v_{M|R}} = \dfrac{dx(t)}{dt} . \vec{e_x} + ...

Les trois points sont pour le reste de l'expression qu'il te reste à établir. Essaye pour cos(\theta(t)) en suivant la formule que je t'ai donné et les indications de mon message à 15:33. Je te promets que ce n'est pas si dur que ça, et qu'avec un peu d'entrainement cela te deviendra complètement naturel. J'aimerais juste que tu trouves l'expression par toi même de :

\dfrac{cos(\theta(t))}{dt} et \dfrac{sin(\theta(t))}{dt}

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 16:29

C'est clair que pour toi ça ne peut etre que facile tu m'as l'air d'être un AS en physique
je pense que la derivée de cos(\theta(t)) peut etre
\frac{d\theta}{dt} * \frac{dcos}{dt}*\theta(t)
encors une fois je pense je me suis gouré lol
c'est surtout la fonction composé que je galère ...

Posté par
Florianbre : Mecanique 28-07-15 à 16:43

C'est une bonne première tentative mais ce n'est pas cela, ne te décourage pas cependant !

Je commence par réécrire la formule générale pour dériver une fonction composée :

(u \circ v(x))' = (u(v(x))' = \dfrac{d(v(x))}{dx} * u'(v(x)) = v'(x) . u'(v(x))

Et je vais prendre un exemple pour te montrer :

Soit f une fonction définie par f(x) = ln(1 + x). Si l'on cherche à dérivée f alors on est bien dans le cas de la dérivée d'une fonction composée. En reprenant la notation ci-dessus on a plus particulièrement :

u = ln(x)
v = 1 + x

On commence donc par calculer v'(x) :

v'(x) = (1 + x)' = 1

On calcule ensuite u'(x)

u'(x) = \dfrac{1}{x}

Et on peut alors exprimer u'(v(x)) :

u'(v(x)) = \dfrac{1}{1 + x}

Et on a donc au final :

f'(x) = 1 .  \dfrac{1}{1 + x} = \dfrac{1}{1 + x}

Maintenant à toi de faire de même avec la fonction cos(\theta(t)). N'ai pas peur du fait que la variable soit notée t au lieu de x c'est juste une habitude liée au fait que t représente le temps. Mais si tu te sens plus à l'aise avec la variable x, commence par dériver cos(\theta(x)). Suis l'exemple que je t'ai donné ci-dessus, pose bien ce que vaut u et v puis procède étape par étape comme je l'ai fait. Dans ta réponse, écrit bien tout ton développement afin que je puisse éventuellement voir où tu t'es trompé si jamais ton résultat est faux.

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 17:01

Il n'y a pas plus parfait que ton explication ! normalement je peux plus me trompé là  !
(cos(\theta(x))' = v'(x) * u'(v(x))
u(x) = cos(x)
v(x) = \theta(x)

u'(x) = \frac{dcos}{dx}
v'(x) = \frac{d\theta}{dx}

(cos(\theta(x))' = \frac{d\theta}{dx} * \frac{dcos}{d\frac{d\theta}{dx}}

J'espère que là c'est bon

Posté par
Florianbre : Mecanique 28-07-15 à 17:04

Je crois qu'on y est presque. Que vaut plus simplement l'expression suivante :

[tex]\dfrac{d(cos(x))}{dx}

? (je suis sûr que tu connais les dérivées des fonctions usuelles)

Posté par
Florianbre : Mecanique 28-07-15 à 17:05

Pardon, je voulais écrire ceci :

\dfrac{d(cos(x))}{dx}

Posté par
lolo77150re : Mecanique 28-07-15 à 17:10

Oui quand meme je connais lol
-sin(x)

Posté par
Florianbre : Mecanique 28-07-15 à 17:15

D'accord. On a donc :

(cos(\theta(x))' = (-1) * \dfrac{d\theta(x)}{dx} * sin(\theta(x))

Peux-tu désormais écrire ce que vaut \dfrac{dcos(\theta(t))}{dt} ? Et n'oublie pas l'indication de l'énoncé qui dit que \omega = \dfrac{d\theta(t)}{dt}

Tu pourras aussi déduire rapidement ce que vaut \dfrac{dsin(\theta(t))}{dt}

Florian

Posté par
lolo77150re : Mecanique 28-07-15 à 17:19

Je vois pas comment tu as fais pour avoir la derivée de cos(theta(x))

Posté par
Florianbre : Mecanique 28-07-15 à 17:25

J'ai posé :

u = cos(x) \\ v = \theta(x)

Donc :

v'(x) = \dfrac{d\theta(x)}{dx}

Puis :

u'(x) = (cos(x)' = (-1) * sin(x)

Et on a donc :

(u(v(x))' = v'(x) * u'(v(x)) = \dfrac{d\theta(x)}{dx} * (-1) * sin(\theta(x)) = (-1) * \dfrac{d\theta(x)}{dx} * sin(\theta(x))

Posté par
lolo77150re : Mecanique 28-07-15 à 17:29

D'accoooord !! c'est bon je vois !
Merci déjà pour ça

Posté par
Florianbre : Mecanique 28-07-15 à 17:33

Voilà, tu peux maintenant normalement répondre à mes questions précédentes que je rappelle ici :

Peux-tu désormais écrire ce que vaut \dfrac{dcos(\theta(t))}{dt} ? Et n'oublie pas l'indication de l'énoncé qui dit que \omega = \dfrac{d\theta(t)}{dt}

Tu pourras aussi déduire rapidement ce que vaut \dfrac{dsin(\theta(t))}{dt}

Posté par
lolo77150re : Mecanique 28-07-15 à 17:44

comme tu l'as écrit en haut \frac{dcos(\theta(t))}{dt} vaut ((-1) * \frac{d\theta(t)}{dt} * sin(\theta(t)))/dt

Posté par
Florianbre : Mecanique 28-07-15 à 17:46

Attention ! Ces deux écritures : \dfrac{d(cos\theta(t))}{dt} et (cos(\theta(t)))' sont équivalentes. Revoie ta réponse, c'est presque cela

Posté par
lolo77150re : Mecanique 28-07-15 à 17:50

\frac{dcos(\theta(t))}{dt} vaut (-1) * \frac{d\theta(t)}{dt} * sin(\theta(t)) *

Posté par
Florianbre : Mecanique 28-07-15 à 17:51

Ok, je suis d'accord avec cela. Et maintenant que vaut \dfrac{dsin(\theta(t))}{dt} ?

Posté par
lolo77150re : Mecanique 28-07-15 à 18:05

u = sin(t)
v = \theta(t)

v'(t) = \frac{d\theta}{dt}
u'(t) = cos(t)

(u(v(x))'= v'(x) * u'(v(x)) = \frac{d\theta}{dt} * cos(\theta(t))  

donc \frac{dsin(\theta(t))}{dt} = \frac{d\theta}{dt} * cos(\theta(t))

Posté par
Florianbre : Mecanique 28-07-15 à 18:23

Juste un petit détail, ne mélange pas les x et les t. Il faudrait que tu écrives : (u(v(x))'= v'(x) * u'(v(x)) = \frac{d\theta}{dx} * cos(\theta(x))  

Mais je suis bien d'accord avec ta conclusion :

\boxed{\dfrac{dsin(\theta(t))}{dt} = \dfrac{d\theta}{dt} * cos(\theta(t))}

Je rajouterais également que dans l'énoncé on te dit que \omega = \dfrac{d\theta}{dt} on peut donc (et plutôt même, on doit) écrire :

\boxed{\dfrac{dsin(\theta(t))}{dt} = \omega * cos(\theta(t))} et \boxed{\dfrac{dcos(\theta(t))}{dt} = (-1) * \omega * sin(\theta(t))}

Maintenant tu as tous les éléments nécessaires pour écrire le vecteur vitesse du point M : \vec{v_{M|R}}.

Posté par
lolo77150re : Mecanique 28-07-15 à 18:48

Oui désolé je me suis rendu compte que quelque minute après et on peut pas modifier donc c'est dommage.
Donc maintenant que j'ai le derivée de cos et sin il faut que je derive tout avec la formule , R compris c'est ça ?

Posté par
lolo77150re : Mecanique 28-07-15 à 19:10

Quand je derive \vec{OM} j'obtient
\vec{v} = \frac{dx}{dt} + (R.(-1).\omega.sin(\theta(t))\vec{ex} + (R.\omega.cos(\theta(t))\vec{ey}
Mais  je crois que ma dérivée n'est pas fini , vu qu'il y a 3 produit donc R.cos(\theta(t)).\vec{ex} j'ai fais
(R.cos(\theta(t))).\vec{ex}
donc pour dabord derivée la parenthese et ensuite le resultat de la derivée , le faire dérivée avec le vecteur ex je sais pas si tu vois ce que je veux dire

Posté par
Florianbre : Mecanique 28-07-15 à 19:39

Oui, normalement il faudrait faire la dérivée d'un produit. Mais cependant, on a les deux choses suivantes qui sont vraies :

\dfrac{dR}{dt} = 0 car la longeur R de la pâle ne dépend pas du temps.

\dfrac{d\vec{e_x}}{dt} = \dfrac{d\vec{e_y}}{dt} = \dfrac{d\vec{e_z}}{dt} = \vec{0} car (O, \vec{e_x}, \vec{e_y}, \vec{e_z}) est ton repère principal.

On a donc bien :

\boxed{\vec{v_{M|R}} = \dfrac{dx(t)}{dt}\vec{e_x} - R.\omega.sin(\theta(t))\vec{e_x} + R.\omega.sin(\theta(t))\vec{e_y}}

Ou encore :

\boxed{\vec{v_{M|R}} = \begin{pmatrix}\dfrac{dx(t)}{dt}- R.\omega.sin(\theta(t))\\R.\omega.sin(\theta(t))\\0\end{pmatrix}}

Maintenant que l'on connait l'expression du vecteur vitesse du point M, j'ai une question pour toi : sais-tu calculer la norme d'un vecteur ? Si ou calcule la norme de ce vecteur vitesse. Le résultat que tu obtiendras (qui est un scalaire) correspondra à la vitesse du point M à tout instant t.

Florian

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !