Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

filtre passe bande ou passe haut

Posté par
speedstar 07-11-12 à 19:36

salut

j'aimerai bien savoir comment faire pour montrer que ce filtre est un passe bande sans faire de calcul BF juste par étude en HF et "par contre moi je l'ai trouvé un passe haut" merci de m'éclaircir étape par étape si possible j'ai vraiment besoin de savoir c'est pour mon TD

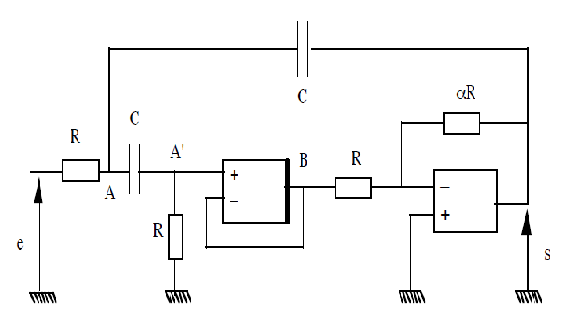
voici l'image de l'exo


merci d'avance

filtre passe bande ou passe haut

Posté par
Marc35re : filtre passe bande ou passe haut 07-11-12 à 20:53

Bonsoir,
On peut dire les choses suivantes.
En BF, les condensateurs ont une grande impédance. On peut les considérer à la limite comme des circuits ouverts. Donc le condensateur C empêche la BF de passer. La structure entre A et B est une structure passe-haut (circuit CR).
Pour la HF, le circuit entre A et B peut être considéré comme ayant un gain de 1. On peut donc le supprimer. Le condensateur entre la sortie et A peut être considéré comme un court-circuit. la tension de sortie est réinjectée sur l'entrée en opposition de phase. Donc la HF est annulée aussi.
Donc c'est un passe-bande.

Posté par
speedstarre : filtre passe bande ou passe haut 07-11-12 à 21:12

merci pour votre réponse détaillée Marc ce que je comprends c'est que en BF le circuit est un filtre passe haut et
en HF c'est un circuit passe bande c'est ça

Posté par
Marc35re : filtre passe bande ou passe haut 07-11-12 à 21:15

Non, un circuit ne peut pas être passe-haut en BF et passe-bande en HF.
Ce que j'ai voulu montrer, c'est que ce circuit ne laisse pas passer les basses fréquences et les hautes fréquences.
En conséquence, c'est un passe-bande.

Posté par
speedstarre : filtre passe bande ou passe haut 07-11-12 à 21:20

oui je m'en doutais
"la tension de sortie est réinjectée sur l'entrée en opposition de phase"
vous pouvez me la réexpliquer svp

Posté par
Marc35re : filtre passe bande ou passe haut 07-11-12 à 21:42

En HF, le circuit entre A et B peut être supprimé parce que c'est un passe-haut et il a un gain de +1 en HF.
Le 2ème ampli op est un montage inverseur large bande (enfin avec des amplis idéaux). Donc la tension de sortie est en opposition de phase avec la tension d'entrée.
Le condensateur étant considéré comme un court-circuit, on fait donc au point A la somme de deux tensions en opposition de phase (en fait, c'est plutôt 2 courants mais le principe est le même).

Posté par
speedstarre : filtre passe bande ou passe haut 07-11-12 à 21:50

Merci c'est plus clair maintenant

et bonne nuit

Posté par
Marc35re : filtre passe bande ou passe haut 07-11-12 à 21:55

Bonne nuit

Posté par
speedstarre : filtre passe bande ou passe haut 07-11-12 à 22:55


si tu me le permets stp pour la tension au point A c'est nulle c'est ça

tu peux bien la démontrer j'ai essayé mais en vain
la fct de transfert de l'AO 2 H=-
la tension au pt A Va=Vs=-Ve
je me suis coincé je vois pas comment Va=Ve+VS=0

Posté par
Marc35re : filtre passe bande ou passe haut 08-11-12 à 11:00

La tension au point A n'est pas nulle.
Je peux faire le calcul complet si besoin est.

Posté par
Marc35re : filtre passe bande ou passe haut 08-11-12 à 11:04

Mais le calcul complet est un peu compliqué...

Posté par
speedstarre : filtre passe bande ou passe haut 08-11-12 à 21:27

si t'as le temps,je veux bien que tu me fasses le corrigé complet
je suis confus car notre professeur s'est trompé peut être en me disant que c'est un filtre passe haut
je savais qu'il a tord mais je sais pas où il a fait l'erreur donc j'aimerai bien le corrigé

et merci

Posté par
Marc35re : filtre passe bande ou passe haut 09-11-12 à 12:31

Voici le calcul en question :
(on peut aussi le résoudre avec les lois des mailles et des noeuds mais c'est plus compliqué et sujet à erreurs...)
théorème de Millman
\Large v_A\,=\,\frac{\frac{v_e}{R_2}\,+\,jC_2\omega\,v_s\,+\,jC_1\omega\,v_{A'}}{\frac{1}{R_2}\,+\,j\left(C_1+C_2\right)\omega}
On a : v_{A'}\,=\,v_B
\Large \boxed{ v_A\,=\,\frac{v_e\,+\,jR_2C_2\omega\,v_s\,+\,jR_2C_1\omega\,v_B}{1\,+\,jR_2\left(C_1+C_2\right)\omega} }

Dans cette expression, il y a deux termes dont on doit se débarrasser : v_B  et  v_A .
Avec l'ampli op de sortie, on peut écrire :
\large \frac{v_s}{v_B}\,=\,\frac{R_4}{R_3}\,=\,\frac{\alpha R}{R}\,=\,\alpha

\large v_s\,=\,\alpha\,v_B\,\Rightarrow\,v_B\,=\,\frac{v_s}{\alpha}
D'autre part :
\Large v_{A'}\,=\,v_A\,\frac{R_1}{R_1+\frac{1}{jC_1\omega}}\,=\,v_A\,\frac{jR_1C_1\omega}{1+jR_1C_1\omega}

\Large v_{A'}\,=\,v_B\,=\,v_A\,\frac{jR_1C_1\omega}{1+jR_1C_1\omega}\,\Rightarrow\,v_A\,=\,v_B\,\frac{1+jR_1C_1\omega}{jR_1C_1\omega}\,=\,\frac{v_s}{\alpha}\,\frac{1+jR_1C_1\omega}{jR_1C_1\omega}

On remplace dans l'expression de vA :
\Large \frac{v_s}{\alpha}\,\frac{1+jR_1C_1\omega}{jR_1C_1\omega}\,=\,\frac{v_e\,+\,jR_2C_2\omega\,v_s\,+\,jR_2C_1\omega\,\frac{v_s}{\alpha}}{1\,+\,jR_2\left(C_1+C_2\right)\omega}

\Large v_s\,\left(1+jR_1C_1\omega\right)\left(1\,+\,jR_2\left(C_1+C_2\right)\omega\right)\,=\,j\alpha R_1C_1\omega\,v_e\,-\,\alpha R_1C_1R_2C_2\,\omega^2\,v_s\,-\,R_1R_2C_1^2\omega^2\,v_s

\Large v_s\,\left(1-R_1R_2C_1(C_1+C_2)\omega^2+j\left(R_2(C_1+C_2)+R_1C_1\right)\omega\right)\,=\,j\alpha R_1C_1\omega\,v_e\,-\,R_1C_1R_2\left(\alpha C_2+C_1\right)\omega^2\,v_s

\Large v_s\left(1-R_1R_2C_1(C_1+C_2)\omega^2+j\left(R_2(C_1+C_2)+R_1C_1\right)\omega\right)\,=\,j\alpha R_1C_1\omega\,v_e

\Large v_s\left(1-R_1R_2C_1(\alpha-1)C_2\omega^2+j\left(R_2(C_1+C_2)+R_1C_1\right))\omega\right)\,=\,j\alpha R_1C_1\omega\,v_e

\Large \frac{v_s}{v_e}\,=\,\frac{j\alpha R_1C_1\omega}{1+j\left(R_2(C_1+C_2)+R_1C_1\right)\omega-R_1R_2C_1(\alpha-1)C_2\omega^2}
On a:
R_1\,=\,R_2\,=\,R
Et :
C_1\,=\,C_2\,=\,C

\Large \frac{v_s}{v_e}\,=\,\frac{j\alpha RC\omega}{1+j\left(2RC+RC\right)\omega-R^2C^2(\alpha-1)\omega^2}

\Large \red{\boxed{\frac{v_s}{v_e}\,=\,\frac{j\alpha RC\omega}{1+j\,3RC\omega-R^2C^2(\alpha-1)\omega^2}}}

Un oeil averti distingue un passe-bande ou un coupe-bande (réjecteur).
Un oeil plus averti voit un passe-bande en remarquant que :
\Large \frac{1}{\alpha RC}\,<\,\frac{1}{RC\,\sqrt{\alpha-1} }        \left(\alpha\,>\,1\right)
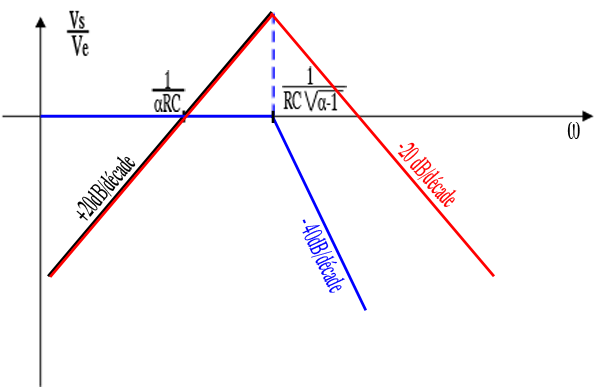
Diagramme de Bode joint.
Pour voir la maximum, il faut calculer la dérivée  \Large \frac{d|\frac{v_s}{v_e}|}{d\omega} .
Pour faciliter le calcul, il est plus simple de calculer  \Large \frac{d|\frac{v_s}{v_e}|^2}{d\omega} .
Et on a :
\Large \frac{d|\frac{v_s}{v_e}|^2}{d\omega}\,=\,\frac{d|\frac{v_s}{v_e}|^2}{d\omega^2}\,\frac{d\omega^2}{d\omega}\,=\,2\,\omega\,\frac{d|\frac{v_s}{v_e}|^2}{d\omega^2} .

Donc on calcule :  \Large \frac{d|\frac{v_s}{v_e}|^2}{d\omega^2} .

Je ne détaille pas le calcul de la dérivée (sauf si nécessaire).
\Large \frac{d|\frac{v_s}{v_e}|^2}{d\omega^2}\,=\,\frac{\alpha^2R^2C^2\left[1-\R^2C^2(\alpha-1)\omega^2\right]\left[1+R^2C^2(\alpha-1)\omega^2\right]}{D^2}
Le signe de la dérivée est le signe de  1-\R^2C^2(\alpha-1)\omega^2
\Large \frac{d|\frac{v_s}{v_e}|^2}{d\omega^2}\,\ge\,0\,\Rightarrow\,1-\R^2C^2(\alpha-1)\omega^2\,\ge\,0\,\Rightarrow\,\omega\,\le\,\frac{1}{RC\sqrt{\alpha-1}}        \left(\alpha\,>\,1\right)  
Donc on a bien un passe-bande.
On peut calculer le gain maximum ( pour  \omega_0\,=\,\frac{1}{RC\sqrt{\alpha-1}} )

\Large \left(\frac{v_s}{v_e}\right)_{\omega_0}\,=\,\frac{j\alpha RC\frac{1}{RC\sqrt{\alpha-1}}}{1+j\,3RC\frac{1}{RC\sqrt{\alpha-1}}-R^2C^2(\alpha-1)\left(\frac{1}{RC\sqrt{\alpha-1}}\right)^2}\,=\,\frac{j \frac{\alpha}{\sqrt{\alpha-1}}}{j\,\frac{3}{\sqrt{\alpha-1}}}

\Large \boxed{\left(\frac{v_s}{v_e}\right)_{\omega_0}\,=\,\frac{\alpha}{3}}

Ouf ! Je suis arrivé au bout...
Je plaisante, j'adore ce genre de calcul... Le plus difficile est de l'écrire en LaTeX...

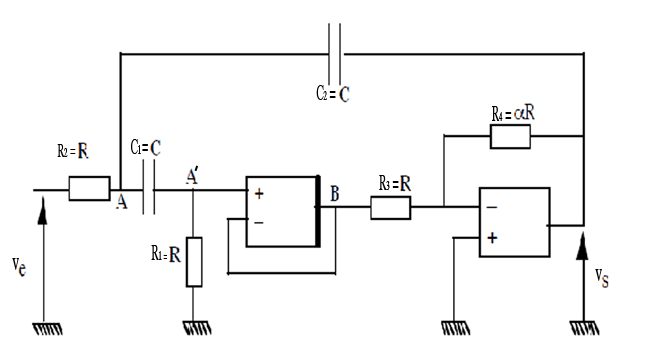
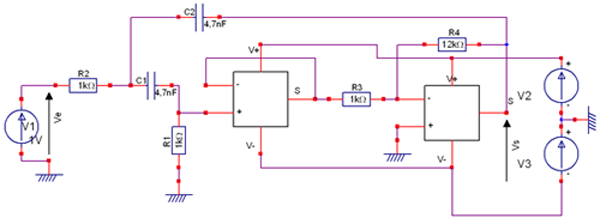
filtre passe bande ou passe haut

filtre passe bande ou passe haut

Posté par
Marc35re : filtre passe bande ou passe haut 09-11-12 à 15:23

Voici une simulation qui correspond au schéma...
- le circuit tout d'abord
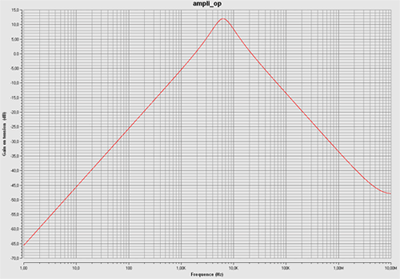
- le diagramme amplitude-fréquence (qui montre que c'est un passe-bande)
(désolé pour la taille mais apparemment je ne peux pas faire plus grand en respectant les contraintes du site)

filtre passe bande ou passe haut

filtre passe bande ou passe haut

Posté par
speedstarre : filtre passe bande ou passe haut 10-11-12 à 08:44

bonjour
merci Marc c'est trop sympa de ta part
j'apprécie vraiment ton aide

Posté par
speedstarre : filtre passe bande ou passe haut 10-11-12 à 09:50

je pense que Vs/Vb=-
th de Millman appliqué à l'entrée inverseuse de L'AO 2 donne
V_=(Vb/R+Vs/R)/(1/R+1/R)
V_=V+=0
donc Vs/Vb=-

Posté par
J-Pre : filtre passe bande ou passe haut 10-11-12 à 10:13

Comportement en (très) haute fréquence :

Les condensateurs se comportent comme des court-circuits et donc on a : VA = VA' = Vs (1)

On a aussi VA' = VB (2) (car l'ampli de gauche est monté en suiveur (gain de +1))

On a donc avec (1) et (2) : VB = VS

Or l'ampli de droite est inverseur et donc VB est de signe contraire à Vs
---
Avec VB = VS alors que VB et Vs sont de signe contraire, la seule possibilité est VB = Vs = 0

Et donc le gain total est nul en haute fréquence.
----------
Comportement en (très) basse fréquence :

Les condensateurs se comportent comme des circuits ouverts (donc comme si ils avaient été supprimés du montages)

On a alors VA' = 0
VB = 0 puisque l'ampli de gauche est monté en suiveur.

et VB = 0 impose VS = 0

Et donc le gain total est nul en basse fréquence.
----------
Conclusion : Seules les fréquences intermédiaires (pas trop petites et pas trop grandes) "passent" à travers de ce filtre.

C'est donc un passe-bande.

Posté par
speedstarre : filtre passe bande ou passe haut 10-11-12 à 10:42

tandis que °=(+1)

Posté par
speedstarre : filtre passe bande ou passe haut 10-11-12 à 10:51

désolé je me suis trompé c'est

w°=1/(+1)RC

Posté par
speedstarre : filtre passe bande ou passe haut 10-11-12 à 10:54

merci JP pour ta réponse effectivement j'ai vérifié par calcul c'est un passe bande

Posté par
Marc35re : filtre passe bande ou passe haut 10-11-12 à 13:55

Oui, j'ai fait le calcul sur une feuille d'abord et ensuite, au lieu de simplement recopier, j'ai voulu vérifier en le refaisant sur l'écran. Je ne trouvais pas la même chose et j'ai choisi ce que je trouvais sur l'écran... Erreur  funeste !...
Effectivement :
\large \frac{v_s}{v_B}\,=\,-\,\alpha

Mais il y a quelque chose qui cloche quand même...
Je revérifie...  

Posté par
Marc35re : filtre passe bande ou passe haut 10-11-12 à 15:23

J'ai refait le calcul mais je ne suis pas satisfait...

\Large \frac{v_s}{v_e}\,=\,-\,\frac{j\alpha RC\omega}{1+j\,3RC\omega-R^2C^2(\alpha+1)\omega^2}

Et la dérivée indique un maximum en :
\Large \omega_0\,=\,\frac{1}{RC\sqrt{\alpha+1}}
Et le gain au maximum :
\Large \left(\frac{v_s}{v_e}\right)_{\omega_0}\,=\,-\,\frac{\alpha}{3}
Et la phase au maximum :
\Large \varphi_{\omega_0}\,=\,-\,\pi

Mais, si le gain (et surtout le gain max) et la phase collent avec les simulations, par contre, la fréquence du maximum ne colle pas avec les simulations...
Alors un problème dans le calcul de la fonction de transfert, dans le calcul de la dérivée ou dans les simulations ?... Je ne sais pas encore...

Posté par
Marc35re : filtre passe bande ou passe haut 10-11-12 à 15:27

A priori, cela ne peut pas venir des amplis op choisis pour la simulation puisqu'ils ont un produit gain-bande (fT) de 50 MHz.
Et les valeurs de R et de C ont été choisis pour avoir un maximum à une fréquence bien inférieure (de 10 à 20 kHz). Cette fréquence dépend de bien sûr.

Posté par
J-Pre : filtre passe bande ou passe haut 10-11-12 à 16:15

Vs = -alpha.VA'

VA'/R = VA/(R+1/(pC))
VA' = VA.pRC/(1+pRC)

Vs = -alpha.VA.pRC/(1+pRC)

I1 = (e-VA)/R  (I dans R de gauche)
I2 = pC.(VA-Vs) (I dans C de contre réaction)
I3 = VA/(R + 1/(pC)) = VA.pC/(1+pRC) (I dans C entre A et A')

I1 = I2 + I3
(e-VA)/R = pC.(VA-Vs) + VA.pC/(1+pRC)
e-VA = pRC.(VA-Vs) + VA.pRC/(1+pRC)
e = -pRC.Vs + VA(1 + pRC + pRC/(1+pRC))
e = -pRC.Vs + VA(1 + 2pRC + p²R²C²)/(1+pRC)
e = pRC.alpha.(VA.pRC/(1+pRC)) + VA(1 + 2pRC + p²R²C²)/(1+pRC)
e = VA(1 + 2pRC + p²R²C²(1+alpha))/(1+pRC)

e = -Vs.((1+pRC)/(pRCalpha)).(1 + 2pRC + p²R²C²(1+alpha))/(1+pRC)

e = -Vs.(1/(pRCalpha)).(1 + 2pRC + p²R²C²(1+alpha)))

Vs/e = -alpha. pRC/(1 + 2pRC + p²R²C²(1+alpha))

et en sinusoïdal :

Vs/e = - alpha. jwRC/[1 - w²R²C²(1+alpha) + 2jwRC]
-----
Sauf distraction... rien relu, as usual  

Posté par
Marc35re : filtre passe bande ou passe haut 10-11-12 à 18:34

Bon, j'ai compris...
C'est une erreur stupide dans les simulations. Le symbole décimal, j'avais mis une virgule dans la valeur de la capacité d'un condensateur à la place d'un point.
Donc tout colle parfaitement...

Posté par
speedstarre : filtre passe bande ou passe haut 11-11-12 à 08:26

bonjour
Marc je sais pas trop ce que tu veux dire mais j'ai aucune idée sur les simulations

Posté par
Marc35re : filtre passe bande ou passe haut 11-11-12 à 14:43

Les simulations, c'est simple en théorie et un peu compliqué en pratique...
Il faut avoir un logiciel de simulation (il en existe des gratuits surtout pour Linux) et des modèles de circuits intégrés et de transistors (modèles Spice en général bien qu'il en existe d'autres). Après avoir construit (dessiné en général), on peut faire une simulation du comportement du circuit. Cela fonctionne plus ou moins bien en fonction des compétences de l'opérateur (et des performances des modèles de circuits intégrés ou de transistors).
En l'occurrence, j'ai fait une erreur stupide (que je ne fais jamais ! ). Pour la valeur de deux condensateurs, j'ai mis "4,7nF" alors qu'il faut mettre "4.7nF".
Le symbole décimal dans le logiciel est le point (symbole anglo-saxon) et pas la virgule (symbole français).
Le logiciel aurait dû dire quelque chose en principe parce qu'il n'a sûrement pas compris. Il a donc pris je-ne-sais quelle valeur pour les condensateurs d'où les résultats bizarres...
Mais ce petit problème étant résolu, je pense que l'on trouve les mêmes résultats tous les deux (après mon erreur de "calcul d'écran").
Tu as vu qu'il s'agit bien d'un passe-bande...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !