Inscription / Connexion Nouveau Sujet
Exercice (hydrostatique)
Bonjour, j'ai besoin d'aide pour un exercice d'hydrostatique.
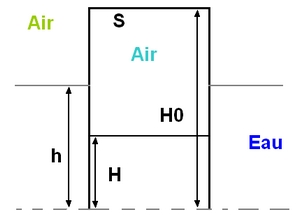
Voici l'énoncé (et le schéma recopié) :
Une cloche cylindrique de masse m dont l'épaisseur des parois est négligeable, est renversée puis plongée verticalement dans une cuve remplie d'eau.
On désigne respectivement par S et H0, la section et la hauteur du cylindre ; par 
et p0, la masse volumique de l'eau et la pression atmosphérique. La cloche s'enfonce dans le liquide en emprisonnant un volume d'air initial égal à son volume intérieur.
La répartition de la masse de la cloche est telle que dans son état final, elle flotte en restant verticale.
L'air emprisonné a une pression finale notée p1 ; on le considèrera comme un gaz parfait et on négligera sa masse volumique devant celle de l'eau.
Dans toute cette partie, la température est supposée constante.
Question 1 : Déterminer l'expression de la pression p1 de l'air dans la cloche.
Question 2 : Quelle est l'expression de la hauteur h de la cloche ?
Pour la 1, j'ai trouvé p1 = p0 + en appliquant la relation fondamentale de l'hydrostatique entre les points : - au contact de l'air (dans la cloche, à hauteur H).
- au contact de l'air (à l'extérieur), à hauteur h.
Pour la 2, je trouve h = H + (m/S), mais je pense qu'aucune de mes réponses n'est exacte.
Merci d'avance, voici le schéma :
Pour la 1, il faut à mon avis utiliser l'expression de la loi des gaz parfaits.
Tu peux considérer que la pression à l'altitude des pointillés est la même, vu qu'on est à l'équilibre (ça flotte).
Du coup:
pression en bas de la cloche = pression à la même altitude sans la cloche
p0 + (eau)gh = p1 + (eau)gH + mg/S
Bon après tu pouvais faire le bilan autrement, en utilisant Archimède ou autre mais tu serais arrivé au même résultat.
Bonjour!
Djyo, tu dis que La pression au point en bas de la cloche (sur les pointillés) est: P1+(rhô)gH + mg/S? Je n'ai pas compris, est-ce que tu pourrais détailler s'il te plaît? 
Bon alors en ayant un petit peu réfléchi:
pour la question 1:
Le cylindre est à l'équilibre. Donc les forces du poids et de la poussée d'Archimède se compensent:
F(p)= mg
F(a)= P1*S-P0*S (différence de pression entre le bas et le faut du cylindre immergé dans l'eau : c'est ça que j'avais oublié)
d'où:
F(p)=F(a)(je parle en norme)
mg=P1*S-P0*S
mg+P0*S=P1*S
mg/S + Po =P1 !
Mais pour la question 2, je ne vois toujours pas désolée.
Pour la première question la pression de l'air
P1V1 = nRT = P0V0
Et du coup P1 = P0.(V0/V1) = P0.(H0/(HO-H))
Pour la méthode avec Archimède:
Poids de la cuve remplie d'air = Force Archimède volume immergé
F(du poids la cuve et de l'air sur l'eau) = mg(h-H)
P1 - P0 = rho(eau)g(h-H)
Pour Hilano, tu as raison je pensais qu'il fallait prendre en compte le poids de la cuve dans les calculs mais en fait celui-ci est contenu dans la pression de l'air (mes souvenirs de PAES ne sont pas toujours super).
P1 + (eau)gH = P0 + (eau)gh
Euh,
F(du poids la cuve et de l'air sur l'eau) = m(vol immergé)g
P1 - P0 = (eau)g(h-H) = mg/S (comme tu l'as montré)
En partant des formules que j'ai démontré:
P1 = P0.(H0/(HO-H))
et P1 + (eau)gH = P0 + (eau)gh
P1 - P0 = (eau)g(h-H)
P0(H0/(HO-H)) = (eau)g(h-H)
P0(H0/(HO-H))/((eau)g) = h-H
h = H + (H0/(HO-H))P0/((eau)g)
Bon après tout dépend d'en fonction de quoi vous voulez votre expression aussi....
Bon encore une erreur, je dois être un peu fatigué:
P1 - P0 = P0(H0/(HO-H)-1) = P0(H/(HO-H))
h = H + P0(H/(HO-H))/((eau)g)
Merci à vous 2 de participer au problème. Ce serait bien que quelqu'un sûr de lui tranche sur ce problème mais apparemment nous sommes tous d'accord pour trouver que p1 = p0 + , ce que je trouve moi en appliquant la relation fondamentale de l'hydrostatique :
p0 + gh = p1 + gH 
p1 = p0 + g(h - H)
p1 = p0 + mVg(h - H)
p1 = p0 +
Pour la 2), je bloque à :
h = H +
Annuler
connectez vous