Bonjour,

1) Sans utiliser la formule de la portée

Dans un référentiel terrestre supposé galiléen. Chute libre (seule force appliquée à la flèche : son poids).
L'axe des abscisses est orienté dans le sens du mouvement, son origine est au départ aux pieds du tireur.
L'axe des ordonnées est orienté vers le haut, même origine.

Au départ les coordonnées de la flèche sont donc {0 ; 1,50}
On souhaite qu'à l'arrivée les coordonnées de la flèche soient {150 ; 0,50}

Vitesse horizontale de la flèche :
Abscisse de la flèche en fonction du temps (pour t 0 et avant l'impact)


Composante verticale de l'accélération de la flèche : -g
Vitesse verticale de la flèche en fonction du temps :
Ordonnée de la flèche en fonction du temps


Equation de la trajectoire de la flèche :


On écrit que pour x = 150 m alors y = 0,50 m



Application numérique (avec g = 9,8 m.s^-2)



soit V₀ 40,96 m.s^-1

2) En utilisant la formule de la portée et avec une lègère approximation.

À l'arrivée l'angle de la flèche avec l'horizontale sera très proche de 30°

Elle doit se trouver 1 mètre sous son niveau de départ. Pour cela elle doit se trouver à son niveau de départ environ 1tan(30°) 1,732 m avant la cible.

Donc la portée doit être de 150 - 1,732 148,268 m

La vitesse initiale V₀ doit être telle que



D'où V₀ 40,96 m.s^-1

Bien sûr, mais tu auras corrigé de toi-même, ce n'est pas (pour la deuxième méthode) :

Citation :
Pour cela elle doit se trouver à son niveau de départ environ 1 tan(30°) 1,732 m avant la cible.

Tout d'abord un tout grand merci ! Mais j'aurais deux questions,

- Dans la première méthode comment trouvez-vous "Vitesse horizontale de la flèche : vo. cos(30°)" ?

- Dans la deuxieme méthode, je comprends le fait que la flèche sera 1m sous son niveau de départ mais j'ai du mal à comprendre la logique du calcul : 1/tan(30°)

désolé si mes questions peuvent paraïtre bêtes :/

Merci d'avance !

Ah Excusez-moi mais j'ai pu trouver ma première question, néanmoins je ne trouve toujours pas ma deuxième question qui est je le rappelle :

Dans la deuxieme méthode, je comprends le fait que la flèche sera 1m sous son niveau de départ mais j'ai du mal à comprendre la logique du calcul : 1/tan(30°)

Voici un schéma.
Attention : les échelles ne sont pas du tout respectées (et donc pas non plus les angles par rapport à l'horizontale)



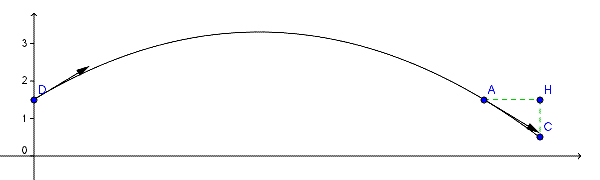
D est le point du départ ; ses coordonnées sont (0 ; 1,5)
C est la cible ; ses coordonnées sont (150 ; 0,5)

A est un point proche de la cible à la même hauteur par rapport au sol (1,5 mètre) que le départ
Les vecteurs symbolisent la vitesse en D et en A
les angles de ces vecteurs avec l'horizontale sont égaux (au signe près)

H est un point au-dessus de la cible, à la même hauteur par rapport au sol que D et A ; ses coordonnées sont donc (150 ; 1,5)

Puisque la distance HC vaut 1 mètre
et que l'angle vaut à très peu près 30°

on en déduit que la distance AH vaut 1 / tan(30°) 1,732 mètre

Wow ! Un grand merci, cela m'éclaire grandement !!!
Sinon pour une toute dernière question, comment peut-on supposer que l'angle à la fin sera de plus ou moins 30° ?

Simple propriété d'une parabole d'axe de symétrie vertical (la trajectoire est une telle parabole) : pour deux points symétriques par rapport à cet axe vertical (donc deux points à la même hauteur au-dessus du sol) les tangentes sont symétriques et donc leurs coefficients directeurs sont opposés. Il en résulte que les mesures des angles de ces tangentes avec une horizontale ont même valeur absolue.

Ok ok un tout grand merci pour tous ces éclaircissements qui m'ont vraiment aidé !!

Je t'en prie.
À une prochaine fois !