Inscription / Connexion Nouveau Sujet
Electrostatique: exercice d'application théorème de Gauss
Voilà je bloque sur un exo
il s'agit d'une distribution de charges électrostatiques à symétrie sphérique constitué par deux sphères,
-la sphère de rayon R, la charge volumique est nulle (  1 )et la charge surfacique est
1 )et la charge surfacique est  o R
o R
-dans la sphère de rayon 2R de meme centre, la charge comprise entre les deux sphères (et dont la densité est fonction de la distance r au centre) est  2 = -
2 = - o
o ou
 o est un constante positive , la charge à la surface de la sphère de rayon 2R est -
o est un constante positive , la charge à la surface de la sphère de rayon 2R est - o R
o R
On se place en coordonnées sphériques (donné par l'exo) donc =r
 r
r
Il faut que je détermine le champ en tout point M de l'espace
En utilisant Gauss :
2 plans de symétrie (M, uz, uthéta) et (M,ur, uz)
Invariance par rotation autour de O
Donc le champ ne dépend que de r et le vecteur est dns la direction de ur
On choisit comme surface de Gauss une sphère de rayon r de centre O
Ensuite il me semble qu'il faut distinguer les cas :
*si r<R alors la charge intérieure Qint=0 donc E(r)=0 (pas sure)
*si R<r<2R alors c'est justement là ou je bloque, j'ai calculer la charge intérieure en considérant le volume chargé entre les deux sphères, et j'ajoute les charges dues à la surface de la sphère de rayon R (Est ce juste ? ), mais comment fait on pour calculer le flux sortant ?? On fait une intégrale dont les bornes sont R et r (variable) ??
* si r>R , il faut ajouter toutes les charges, et pour le flux je trouve 16 E(r) R^2 mais ça me semble faux ...
Pouvez vous m'aider SVP ?
Edit Coll :
Bonjour Samossa,
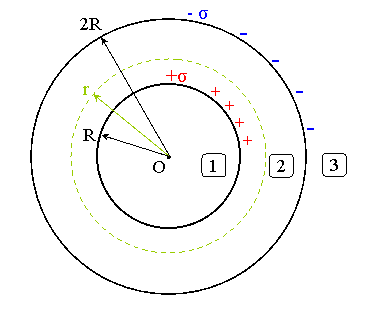
voici les explications, a suivre avec le schema ci-dessous :
J'appelle  =
=  0R la densite superficielle de charge sur la sphere de rayon R, sachant que sur l'autre la densite superficielle est -
0R la densite superficielle de charge sur la sphere de rayon R, sachant que sur l'autre la densite superficielle est -  . L'espace est divise en trois regions : (1), l'interieur de la sphere de rayon R ; (2), l'espace compris entre les deux spheres ; (3), le reste.
. L'espace est divise en trois regions : (1), l'interieur de la sphere de rayon R ; (2), l'espace compris entre les deux spheres ; (3), le reste.
1) calcul des charges :
Sur la sphere de rayon R, la charge repartie en surface est Q1s =  .4
.4 R2 = 4
R2 = 4
 0R3 ;
0R3 ;
Sur la sphere de rayon 2R, la charge repartie en surface est Q2s = - .4
.4 (2R)2 = - 16
(2R)2 = - 16
 0R3 ;
0R3 ;
Entre les deux spheres il faut prendre la densite volumique de charges  (x) = -
(x) = - 0.R2/x2, utiliser l'element de volume en coordonnees spheriques avec symetrie spherique soit d
0.R2/x2, utiliser l'element de volume en coordonnees spheriques avec symetrie spherique soit d = 4
= 4 x2.dx, et integrer de x = R a x = 2R. Je te passe le detail du calcul, on trouve Q2 = -4
x2.dx, et integrer de x = R a x = 2R. Je te passe le detail du calcul, on trouve Q2 = -4
 0R3.
0R3.
Pour trouver le champ dans la region 2, on aura besoin aussi de la charge q2(r) contenue entre la sphere de rayon R et celle de rayon r ; en integrant l'expression precedente entre x = R et x = r, on obtient q2(r) = -4
 0R2(r - R). Attention, les majuscules et minuscules pour R et r sont importantes.
0R2(r - R). Attention, les majuscules et minuscules pour R et r sont importantes.
2) Expression du champ electrostatique :
Le probleme est a symetrie spherique, donc la sphere de Gauss  est une sphere centree sur O et de rayon r. Le flux de E sortant de cette sphere est
est une sphere centree sur O et de rayon r. Le flux de E sortant de cette sphere est  (r) = E(r).4
(r) = E(r).4 r2.
r2.
Il ne reste plus qu'a comparer cette expression avec la quantite de charges Q enfermee dans la sphere de Gauss divisee par  0 pout obtenir la norme du champ electrostatique en tout point M a la distance OM = r du centre de symetrie O. On obtient en effet E = Q/(4
0 pout obtenir la norme du champ electrostatique en tout point M a la distance OM = r du centre de symetrie O. On obtient en effet E = Q/(4
 0r2).
0r2).
Je n'etudie pas tout de suite ce qui sepasse a la traversee des deux surfaces chargees. les inegalites ci-dessous sont donc strictes.
3a) region 1, r < R :
Pas de charges dans  , Q = 0 donc E1 = 0.
, Q = 0 donc E1 = 0.
3b) region 2, R < r < 2R :
Q = Q1s + q2(r), soit E2(r) = 1/(4
 0r2).(8
0r2).(8
 0R3 - 4
0R3 - 4
 0R2r).
0R2r).
3c) region 3, r > 2R :
Q = Q1s + Q2 + Q2s, ce qui apres simplification donne E3(r) = - 4 0R3/(
0R3/( 0r2).
0r2).
4) traversee des surfaces chargees :
Rappel : a la traversee d'une surface contenant des charges reparties avec la densite superficielle  . le champ subit une discontinuite de
. le champ subit une discontinuite de  /
/ 0.
0.
a) Traversee de la sphere de rayon R :
Pour r < R et r  R, l;e champ est nul ; pour r > R et r
R, l;e champ est nul ; pour r > R et r  R, E2 tend vers la valeur E2(R) =
R, E2 tend vers la valeur E2(R) =  0R/
0R/ 0 =
0 =  /
/ 0. Donc c'est verifie.
0. Donc c'est verifie.
b) Traversee de la sphere de rayon 2R :
Pour r < 2R et r  2R, E2 tend vers 0 (en effet, Q1s et Q2 sont egales et de signe oppose). Pour r > 2R et r
2R, E2 tend vers 0 (en effet, Q1s et Q2 sont egales et de signe oppose). Pour r > 2R et r  2R, E3 tend vers la valeur -4
2R, E3 tend vers la valeur -4 0R3/[
0R3/[ 0.(2R)2] = -
0.(2R)2] = -  0R/
0R/ 0, donc -
0, donc -  /
/ 0. Verifie aussi.
0. Verifie aussi.
Si tu as des questions, n'hesiet pas a poster.
Prbebo.
Bonjour Samossa,
alors, que pense-tu de la solution que j'ai donnee a ton probleme ? Il semblerait que ton remerciement ait saute, lui aussi...
Prbebo.
Bonjour Prbebo
Je ne m'appelle pas Samossa mais je te remercie quand même, ton explication m'a bien aidé !
gus3000
Bonjour gus3000,
je suis satisfait de voir que ce corrige, dont la frappe m'a pris presque une heure, a fini par servir a quelqu'un. En effet, avec Samossa j'ai vraiment eu l'impression de parler dans le vide.
Si tu as d'autres pb, avec l'electrostatique ou autre, n'hesite pas a mettre un enonce sur ce forum.
Prbebo.


